(Сентябрь 2012)
Совсем еще молодое, но уже очень горячее направление исследований в физике – «топологические изоляторы» – открывает новые захватывающие перспективы для развития электронных технологий. Попутно раскрывается и кое-что неожиданное о тайнах устройства вселенной…
Представлены к награде
Летом каждого года, строго в один и тот же день 8 августа в мировом сообществе физиков происходит очередное вручение престижной «цеховой» премии – медали Дирака.
Эта награда была учреждена в середине 1980-х годов Международным институтом теоретической физики в г. Триесте, Италия, и присуждается ученым-лауреатам на основе двух основных принципов: (а) за выдающийся теоретический вклад в развитие физической науки; (б) медали Дирака удостаиваются лишь те, кто прежде не получал других знаменитых наград, таких как Нобелевская премия, медаль Филдса, премия Вольфа.
(К счастью для медалистов, весьма почетная премия Дирака никак не препятствует получению в дальнейшем вышеперечисленных наград.)
Три последние медали, врученные 8 августа 2012 (день 110-й годовщины со дня рождения одного из главных основоположников квантовой физики П.А.М. Дирака), особо примечательны вот по какой причине.
В науке очень нечасто случается так, чтобы сугубо теоретически открытый физиками новый материал был почти сразу же обнаружен экспериментально и, более того, быстро нашел множество чрезвычайно перспективных применений в технологиях электроники и других практических приложениях.
Все нынешние лауреаты – Д. Холдейн, Ч. Кейн и Ш. Чжан (Duncan Haldane, Charles Kane, Shoucheng Zhang) – независимо друг от друга работают в разных университетах США над развитием квантовой теории конденсированного состояния вещества. А медали Дирака они удостоены как исследователи, существенно продвинувшие наше понимание весьма необычного типа материала, для которого теперь уже общепринятым стало название «топологический изолятор».

Чтобы в общих чертах дать представление о необычности топологических изоляторов, достаточно перечислить их отличительные особенности.
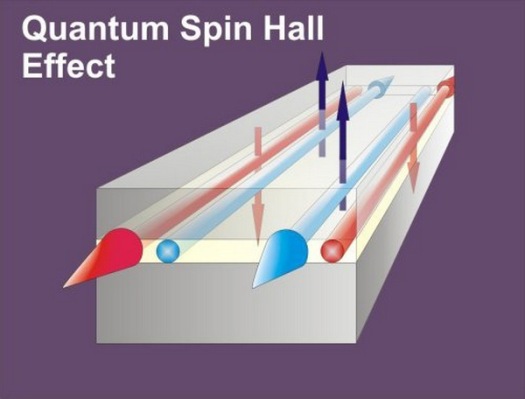
Как можно понять уже из названия, материалы такого типа принято относить к изоляторам или, иначе, диэлектрикам либо полупроводникам, не пропускающим, вообще говоря, через себя электрический ток. Но за одним очень важным исключением – в своем тончайшем поверхностном слое этот материал проводит ток как металл (и даже лучше).
Для наглядности можно представлять себе топологический изолятор (ТИ) чем-то вроде куска дерева, покрытого сверху медью, только в данном случае речь идет не о двух веществах, а об образце одного и того же материала. Причем материала такого, в котором особое квантовое состояние электронов в поверхностном слое делает их не просто переносчиками тока, но «топологически защищенными» переносчиками.
В более доходчивых общечеловеческих словах это означает, что данные квантовые состояния электронов чрезвычайно стабильны – в отличие от обычных состояний частиц на поверхности, здесь они не могут быть разрушены загрязнениями, неоднородностями или другими несовершенствами материала.
Почему в характеристики состояния электронов привлекают раздел геометрии, именуемый топология, пояснить удобнее чуть позже.
Здесь же важно подчеркнуть, что топологические свойства этого материала могут устойчиво сохраняться вплоть до высоких температур. А это означает богатый потенциал ТИ для применения в самых разнообразных практических приложениях микроэлектроники и компьютерной техники – от очень быстрых, энергетически экономичных межсоединений, процессоров, памяти и вплоть до топологических квантовых компьютеров.
История происхождения
По давно сложившейся в науке традиции обычный порядок вещей в открытиях таков, что сначала у экспериментаторов в опытах и наблюдениях обнаруживается нечто новое, а уже затем теоретики дают этому объяснение. Если могут, конечно.
Классический пример такого порядка – явление сверхпроводимости. Впервые данный эффект был обнаружен еще в 1911 году, однако теоретикам понадобилось затем почти полвека, чтобы прийти к более или менее удовлетворительному объяснению феномена.
Однако даже это, в целом утвердившееся объяснение оказывается неприменимо ко всем известным типам сверхпроводящих материалов (физика высокотемпературной сверхпроводимости, в частности, остается неясной по сию пору).
В науке имеется, конечно, не так мало сюжетов и с противоположным порядком событий – вроде создания атомной бомбы, к примеру.
Однако история с открытием феномена под названием топологический изолятор все равно стоит совершенно особняком. Уже по той, хотя бы, причине, что в течение очень долгого времени у физиков вообще не было никаких причин предполагать, будто странные такого рода материалы могут существовать в природе.
Ситуация изменилась благодаря графену – другому удивительному материалу, необычные квантовые свойства которого были теоретически описаны еще в середине XX века, однако реально получить его для экспериментальных исследований удалось лишь к началу XXI столетия.
Среди массы ученых, энергично занявшихся всесторонним изучением этого новомодного материала был и Чарльз Кейн, физик-теоеретик Пенсильванского университета в Филадельфии.
В 2004 году, занимаясь обсчетом свойств графена (тончайшего, в один атом толщиной, листа из атомов углерода), Кейн и его группа обнаружили феномен, весьма напоминающий по своим чертам известный с 1980-х годов квантовый эффект Холла.
Суть его в том, что при весьма особых условиях – очень низких температурах и сильном воздействии внешних магнитных полей – электроны в тонкопленочных материалах от обычных хаотических движений переходят в режим коллективного упорядоченного движения, управляемого квантовой механикой.
Для условий графена, однако, коллективное поведение электронов выглядело не совсем так же, как при квантовом эффекте Холла. Но самое главное, с опорой на более ранние результаты Дункана Холдейна группе Кейна удалось показать, что помимо графена могут существовать и другие тонкопленочные материалы с подобным поведением.
Причем для них уже не требовалось ни огромное внешнее магнитное поле, ни сверхнизкие температуры. Из расчетов получалось, что такого рода материалы могли бы порождать согласованное поведение электронов благодаря магнитному полю от ядер своих собственных атомов – и не исключено, что даже при комнатной температуре.
Скоординированные в своем поведении электроны почти всегда жестко ограничены в движениях внутри материала – они согласованно вращаются по сути лишь на одном месте, по орбитам вокруг своих ядер.
Самое же любопытное, однако, происходит с теми электронами, что находятся на самом краю пленки – здесь они вынуждены перескакивать вдоль этой границы материала от одного атома к другому.
Итоговым же результатом становится то, что тончайшие образцы материала-изолятора проводят электричество по самому своему краю – и только по этому краю. Причем изменение проводимости здесь происходит лишь строго дискретными квантовыми шагами, подобно тому, что наблюдается в квантовом эффекте Холла…
Новаторская работа Кейна и его коллег была замечена в сообществе ученых практически сразу. Вскоре Джоэлу Муру (Joel Moore) и его группе в Калифорнийском университете Беркли, двигаясь от работы Кейна удалось показать, что и трехмерные образцы материала способны также демонстрировать аналогичные квантовые эффекты.
Хотя здесь согласованное движение электронов проводимости вдоль поверхности 3D-материала оказывалось более сложным, нежели в случае плоского 2D-листа, проанализированного Кейном.
От команды Мура тогда же пошло и новое название для гипотетического материала. Поначалу, с подачи Кейна, этот феномен именовали довольно витиевато – «новыми топологическими инвариантами Z2» (обозначая этим особые квантово-механические свойства, которые заставляют электроны прыгать вдоль края).
Мур рассказывает о рождении термина так: «В какой-то момент нас просто стало утомлять печатать все эти слова, вот мы и дали свое название ‘топологический изолятор’… Я не знаю, насколько этот термин выглядит что-то более там разъясняющим, но по крайней мере он покороче».
Еще одна группа теоретиков – под руководством Шоучэн Чжана в Стэнфордском университете, Калифорния – тем временем занялись исследованиями практического аспекта: какого рода реальные материалы могли бы оказаться топологическими изоляторами.
В большинстве материалов, как обнаружила эта команда, связь между электронами и ядром была слишком слаба, чтобы воспроизводить поведение ТИ. Однако по мере того, как ядро атома становится тяжелее, становится сильнее и нужная связь.
В 2006 году Чжанг представил расчеты, предсказывающие, что один конкретный материал – кристалл из тяжелых элементов ртути и теллура – действительно смог бы продемонстрировать нужный трюк.
Уже на следующий год опытная команда физиков-экспериментаторов Лоуренса Моленкампа (Laurens Molenkamp) в Университете Вюрцбурга, Германия, сумела вырастить тонкий слой кристалла теллурида ртути и на опыте продемонстрировать правоту теоретиков. Вдоль края материала проводимость материала действительно прыгает от одного квантового значения к другому.
Хотя эксперимент Моленкампа и доказал любопытные предсказания теоретиков, однако сам по себе он еще не вызвал значительного возбуждения в научных кругах. Кристаллы теллурида ртути чрезвычайно сложны в производстве, поскольку их приходится выращивать послойно с опорой на весьма трудоемкий процесс под названием молекулярно-пучковая эпитаксия (МПЭ).
Кроме того, итоговый результат еще нельзя было назвать чистым топологическим изолятором, потому что данные кристаллы некоторый электроток проводят и внутри себя.
Но процесс, как говорится, пошел. Так что вскоре, в 2008, были обнаружены новые композитные материалы на основе висмута, которые легко выращивать или же можно покупать для исследований уже готовые. И что особенно важно, с ними уже не нужны кристаллы высочайшей чистоты, чтобы увидеть работу квантовых топологических эффектов в действии.
С компаундов на основе висмута, собственно, и принято отсчитывать «восход эры ТИ» – взрыв экспериментальных и теоретических работ, продолжающих бурное развитие и в настоящее время.
Топологические инварианты
Принципиальная особенность топологического изолятора в том, что его проводящая поверхность – это по своим свойствам далеко не обычный металл.
Здесь важнейшую роль играет спин электрона, квантовая характеристика частицы, позволяющая представлять ее как вращающийся волчок, ось которого имеет строго определенное направление. В условиях ТИ направление движения поверхностного электрона и ориентация его спина жестко связаны (заперты) и изменяются только согласованно друг с другом.
Одним из следствий данной связи, в частности, является то, что ток электронов на поверхности топологического изолятора одновременно происходит в двух взаимно противоположных направлениях. То есть частицы со спином «вверх» движутся по краю в одну сторону, а со спином «вниз» – в обратную.
Но еще более удивительное, наверное, предсказание для свойств ТИ заключается в том, что строго сориентированные поверхностные электроны не могут быть рассеяны дефектами или другими возмущениями той среды, в которой движутся.
По этой причине электроны испытывают очень небольшое или даже вообще – как в сверхпроводниках – никакое сопротивление среды в процессе своего продвижения. На жаргоне ученых, такие поверхностные состояния электрона являются «топологически защищенными», то есть они не могут рассеиваться без нарушения правил квантовой механики.
В ограниченных объемах данной статьи, конечно же, вряд ли уместны попытки пересказывать квантовую теорию твердого тела, основы зонной структуры для энергетического спектра материалов и непосредственную взаимосвязь этого подхода с геометрией.
Однако для общего понимания того, откуда в названии ТИ берется сам термин «топологический», все же полезно рассмотреть принципиальные особенности соответствующей математической дисциплины.
По определению, топология – это ветвь математики, занимающаяся такими аспектами формы, которые не могут быть фундаментально изменены растяжением, сжатием или изгибами. Формулируя иначе, для топологии несущественны расстояния, однако ее особенно интересуют такие особенности формы, которые именуются инвариантами и остаются неизменными при всевозможных гладких преобразованиях (т. е. без применения разрезов и склеиваний).
Благодаря инвариантам удобно классифицировать и различать действительно разные формы, не преобразуемые одна в другую. Типичным примером топологического инварианта является дыра пончика (тора). Вы без труда можете деформировать форму пончика до формы кружки. То, что было дырой в пончике, теперь становится дырой в ручке кружки. Таким образом, для математики форма кружки и форма пончика топологически неразличимы.
Но этот пример, к сожалению практически никак не поясняет, каким образом топологические инварианты появляются в физике экзотических материалов, вроде ТИ, да еще и существенно влияют на характер их электрической проводимости.
Несколько более удачным, наверное, примером может служить карта станций метрополитена города Москвы. Математически подобный объект именуется графом, и с точки зрения топологии пример хорош тем, что реальные физические расстояния между станциями здесь не существенны, а важны лишь линии взаимосвязей станций друг с другом и узлы пересадок, объединяющие линии в единую сеть.
Понятно, наверное, что эти связи остаются неизменными при любых растяжениях и сжатиях графа. Ну а особо важным инвариантом для карты метро Москвы можно считать кольцевую линию. Если на этой линии пассажир сел в поезд, то лишь здесь он имеет возможность проехать через станции всех прочих линий и попутно объезжать город по замкнутой траектории кольца.
Из этого примера будет проще, наверное, представить, как топология поверхностей в воображаемом пространстве энергетических состояний электронов способна формировать для них зону весьма особого квантового состояния.
В случае ТИ благодаря инвариантам этой топологии электроны на физической поверхности материала становятся примечательно нечувствительными к загрязнениям среды и другим возмущающим эффектам, которые вообще говоря имеют тенденцию разрушать их свойство проводимости.
Иначе говоря, электроны топологически сопротивляются фундаментальным переменам их свойств – примерно также, как это делает дыра в растягиваемом и сжимаемом резиновом кольце.
И как результат, поверхностные электроны – в зависимости от ориентации своего спина – свободно текут по поверхности ТИ в противоположные стороны. Примерно также, как едут пассажиры на поездах кольцевой линии московского метро – во встречном направлении, в зависимости от того, с какой стороны перрона они вошли в вагон.
Надежно и практично
Итак, особо сильное «спин-орбитальное взаимодействие» (жесткая связь между ориентацией спина и направлением его движения) в атомах тяжелых элементов, вроде висмута, может порождать топологические инварианты, приводящие к самым радикальным последствиям для свойств материала.
Говоря упрощенно, полупроводник становится изолятором внутри и «металлическим» проводником на поверхности. При этом, благодаря спин-орбитальному взаимодействию и его следствиям, свойства материала оказываются весьма привлекательными с точки зрения практических приложений.
Во-первых, важен магнитный аспект ТИ. В обычном металле электрон, движущийся в конкретном направлении, может иметь спиновую ось, указывающую в любом направлении.
А в металлической поверхности ТИ все электроны сориентированы осями идентично и строго в соответствии с тем направлением, в котором они движутся. И в ситуации, когда они все движутся в одном и том же направлении – как часть электротока – такие электроны коллективно действуют как магнит.
Исследователями уже предложены несколько устройств, которые используют преимущества этой сильной связи между плотностью тока и магнитным моментом. Представим, к примеру, нанесение магнитного слоя (вроде тех, что используются для хранения битов на пластинах жесткого диска) на поверхность топологического изолятора.
Пропуская небольшой ток в ТИ, можно эффективно считывать биты, хранящиеся в магнитном слое. А при подаче тока более сильного напряжения спиновая плотность, наводимая в топологическом изоляторе, могла бы переключать состояние магнитных битов, таким образом делая перезапись содержимого.
Далее, топологические изоляторы работают поразительно надежно в условиях реальной эксплуатации. Они сохраняют свое уникальное сочетание изоляционных и поверхностно-проводящих характеристик даже в тех случаях, когда материал засорен инородными включениями и находится в условиях электромагнитного шума окружающей среды.
Эта способность ТИ – еще одна манифестация известного парадокса квантового поведения, непредсказуемого на квантовом микроуровне, однако высоко надежного на макроуровне коллективного поведения частиц.
Такая стабильность эффекта была очевидна уже в сверхпроводимости – первом из обнаруженных феноменов квантового поведения материи в макроскопических масштабах. А также в близко связанном с этим феноменом явлении сверхтекучести – способности сверхохлажденного гелия к течению без вязкости.
Как супержидкости, так и сверхпроводники демонстрируют свои свойства в реальных материалах, которые с неизбежностью содержат в себе неоднородности и посторонние включения.
Отсюда понятно, наверное, что когда индустрия приближается к созданию микроэлектроники наномасштабов (плюс вынашиваются амбициозные проекты типа квантовых компьютеров), крайне важными и заманчивыми выглядят возможности ТИ.
То есть материалов, обеспечивающих доступность таких каналов проводимости, которые ничем не нарушаются и будут стабильно работать в независимости от того, что на хрупком микроуровне этому все время препятствуют какие-нибудь неискоренимые помехи.
Еще один важный и довольно необычный аспект ТИ – эффект нулевой массы. Согласно известному факту квантовой физики, электрон, движущийся в полупроводнике, имеет такую эффективную массу, которая может очень сильно отличаться от его массы в вакууме. Причем отличия даже в 10 раз в ту и другую сторону здесь не являются чем-то необычным.
Для образной иллюстрации эффекта, электрон здесь – словно лошадь, которая может превращаться либо в слона, либо в собаку. И даже более того, для экзотических условий ТИ установлено, что электроны на поверхности данного материала имеют эффективную массу нуль.
Примечательно, что столь необычный эффект отмечен уже не впервые. Электроны с нулевой массой ранее были открыты в другом экзотическом материале – в листе графена, или пленке одноатомной толщины из гексагонально расположенных атомов углерода.
Происхождение эффекта нулевой массы в графене, согласно современным представлениям, не имеет никакого отношения к спину электрона. Однако собственно эффект имеет для обоих материалов похожие технологические последствия – коль скоро позволяет проектировать на их основе очень быстрые электронные устройства.
Например, не так давно учеными IBM был продемонстрирован первый 100-гигагерцевый транзистор с конструкцией на базе графена.
Эффект нулевой массы позволяет прогнозировать для ТИ и другие приложения, менее очевидные, чем быстрые устройства. Например, в материале с «нулевой массой» количество носителей заряда намного более чувствительно к применению электрического поля, нежели в типичном полупроводнике.
Этот процесс манипуляций проводимостью известен как «полевые присадки» (field doping) – по аналогии со стандартным процессом управления плотностью носителей при помощи химических присадок – однако имеет преимущество, которого нет у присадок химических.
В ТИ вы можете быстро обращать воздействие полевой присадки простым изменением электрического поля, в то время как химическая присадка по самой сути своей вещь постоянная.
И наконец, перечисляя всевозможные будущие приложения топологических изоляторов, было бы странно не упомянуть и наиболее очевидное из них – спинтронику.
Исследователи многих стран уже довольно давно пытаются создать радикально новое направление электроники – спинтронные устройства, которые для оптимального хранения и передачи информации использовали бы спин электронов, а не их перемещения.
Хрупкая природа трудно управляемых квантовых эффектов и здесь очень сильно тормозит разработку практичных устройств, ну а по сути спиновая природа феномена ТИ и здесь ныне обещает радужные перспективы прогресса.
Майорана и квантовый компьютер
Еще одно очень заманчивое – но пока что представляющееся скорее гипотетическим, нежели практическим – приложение топологических изоляторов связывают с созданием квантового компьютера. Если чуть точнее, то речь идет о конструкции так называемого топологического квантового компьютера на основе фермионов Майораны.
Загадочные майорановские частицы, как и судьба их автора, сами по себе составляют одну из наиболее таинственных историй в физике XX века.
Необычные по своим свойствам фермионы – как одно из допустимых решений уравнения Дирака – были впервые предсказаны выдающимся итальянским физиком Этторе Майораной в 1937 году.
Причем сделано это было незадолго до того, как ученый, едва перешагнув рубеж 30-летнего возраста, загадочно и навсегда исчез в 1938 году с морского парома, шедшего из Неаполя в Палермо.
По сию пору не обнаруженные в природе фермионы Майораны интересны не только потому, что они являются своими собственными античастицами, но также по той причине, что они, согласно расчетам, должны быть чрезвычайно устойчивы к шумам и воздействиям окружающей среды.
Майорановские фермионы, иными словами, можно было бы использовать для надежного хранения и передачи квантовой информации – как ни возмущал бы и ни искажал ее внешний мир (гигантская сложность этой проблемы висит как проклятие над всеми, кто пытается построить практичный квантовый компьютер).
Хотя абсолютно достоверного доказательства существованию фермионов Майораны получить пока не удается, теоретики рассчитали, однако, что похожие на частицы возбуждения среды – или квазичастицы – которые ведут себя как фермионы Майораны, могли бы появляться при манипуляциях с топологическим изолятором.
В частности, они должны существовать на границе таких областей, где ТИ – материал, проводящий ток лишь на поверхности – размещен рядом с обычным сверхпроводником. Такого рода квазичастицы также именуют «модами нуль-энергии».
По случайному совпадению, в том же августе 2012, когда первооткрыватели ТИ были удостоены медали Дирака, появилась и публикация о том, что физики Стэнфордского университета обнаружили экспериментальные признаки фермиона Майораны.
Ученые изучали свойства так называемого джозефсоновского перехода в устройстве новой, не совсем обычной конструкции – где между двумя сверхпроводящими контактами, словно ломтик сыра в сэндвиче, был проложен слой топологического изолятора.
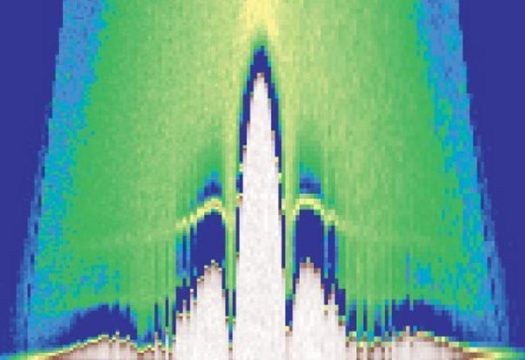
В поведении данной системы исследователи обнаружили существенные отклонения от того, что приходится наблюдать в обычном джозефсоновском переходе. А выявленные различия, как они полагают, хорошо объясняются в терминах квазичастиц типа Майорановских фермионов.
Конечно же, от этого результата еще очень далеко до практичного квантового компьютера, в котором кубиты будут реализованы на основе майорановских квазичастиц, способных своими топологическими свойствами надежно защищать информацию от искажений.
Однако есть немало ученых, считающих что двигаясь именно по этому пути – через конструкции топологической защиты – труднейшую задачу все-таки удастся решить. Потому что именно так, считают они, стабильные квантовые системы (все разновидности окружающей нас материи) реализованы в природе.
И кое-что еще…
Надежды на обнаружение с помощью ТИ экзотических частиц Майораны – это далеко не все, чем еще интересен новый материал для теоретиков за пределами сугубо практических приложений.
У исследователей есть веские основания полагать, что режимы коллективного поведения электронов внутри топологических изоляторов способны моделировать довольно обширный ряд никогда не виданных прежде объектов, предсказанных ранее в физике частиц и высоких энергий.
Среди таких кандидатов, в частности, называют аксионы – гипотетические частицы, предсказанные в 1970-е годы для красивого разрешения некоторых нестыковок в теории. Или, скажем, магнитные монополи (отдельные друг от друга полюса магнетизма), давным-давно предсказанные еще Полем Дираком, однако так и не обнаруженные экспериментально.
Нельзя сказать, что столь богатая мимикрия ТИ – это полный сюрприз. Как поясняет ситуацию нобелевский лауреат Фрэнк Вильчек, коллективные движения электронов в квантовой физике могут быть описаны лишь довольно небольшим количеством переменных, так что «имеется всего лишь несколько типов уравнений, которые можно для них записать и которые действительно просты».
А потому теоретикам, исследующим топологические изоляторы и физику частиц, в итоге почти неизбежно было суждено встретиться в одном и том же месте.
Одним из самых любопытных, наверное, открытий, совсем недавно сделанных на данном «пути объединения», стала работа исследователей из Института ядерной теории в Сиэттле (David Kaplan, Sichun Sun), согласно которой буквально все пространство-время вселенной можно рассматривать как топологический изолятор.
В качестве красивого следствия такого подхода авторами предлагается естественное объяснение для одной из глубочайших загадок современной физики – почему в природе наблюдается ровно три поколения элементарных частиц.
Подробнее об этой и других созвучный ей работах, исследующих космологическую, так сказать, значимость ТИ и графена, можно прочесть в материале «Вселенная как топологический изолятор».
В заключение же осталось отметить, что топологические изоляторы и графен, по мнению многих физиков, наши потомки будут вспоминать как первые материалы, обнаруженные экспериментально в XXI веке и по своему значению сравнимые с великими научными достижениями века XX.